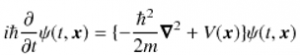シュレディンガーの波動方程式
1926年、シュレディンガーはド・ブロイの発想をもとにして物質波の波動方程式を構築しました。それが「シュレディンガー方程式」です。
線形代数との深い関係
「線形代数」というのは数学の一部門で、行列の計算などを扱います。 線形代数と量子力学は別の学問ですが、両者には強い関連があります。
行列は、単に数が沢山並んだだけのものと思いがちですが、実は作用素と同じ働きをもっています。行列は、あるベクトルを入力として受け取り、それを別のベクトルに変形して出力します。行列に並んだ沢山の数字が、その変換規則を指定します。
ベクトルを行列に作用させることを、数学の世界では、ベクトルに行列を「掛ける」といいます。 その結果は「別のベクトル」になります。 行列を「掛ける」ことは、作用素を「作用」させることと同じことです。
そして、特殊な場合に、掛けた結果が入力ベクトルと同じになることがあります。 この入力ベクトルは、その行列に対して固有状態になっているわけです。 このような特別なベクトルのことを、「固有ベクトル」と呼びます。
ある行列の固有ベクトルを求めるための方程式を、固有方程式と呼びます。 この式は、量子力学の波動方程式と同じ型です。
式の形だけでなくて、意味も同じです。 固有ベクトルを求めるには、上から任意のベクトルを掛けてみて、その結果が同じになるものが見つかるまで、どんどん探索を続けるのです。 そして、固有ベクトルを見つけることが できれば、それが行列のデータの「本質」を表してくれるという点も同様です。
行列の固有ベクトルは、行列の本質を「昇華された形」で表します。
固有方程式とは?
線形代数における固有方程式とは、与えられた行列に対し、掛けても方向が変化しないような特別なベクトル(固有ベクトル)を求めるための方程式のことです。
行列「A」と、ベクトル「x」と、普通の数「λ」があって、これらの間に「Ax=λx」という式を満たすような、「x」と「λ」を求めるという方程式です。この方程式での未知数は「x」と「λ」の2つです。「A」だけが判っていて、「x」も「λ」も未知です。未知数が多すぎて、解けないのではないかと感じられるかもしれませんが、解くことができます。
「Ax=λx」の「λ」をちょっと無視して、「Ax=x」だと考えると、この式の本質がよくわかります。 つまり、ある行列「A」が与えられたときに、それに掛けても(作用しても)方向が変化しないようなベクトル「x」を探す(「x」の長さは無視して)わけです。そして「x」の方向さえ決まれば、そのとき「x」の「長さ」がどのくらい変化するのか、その変化倍率を表す「λ」(これを固有値と呼びます)も、自動的に決まるのです。
量子力学の波動方程式も、これと全く同じ構造になっています。
ところで、波動関数の解釈については、色々な考えが提案されました。
粒子である電子を波として扱う。そうして計算すると、電子の波の形を決定することができる。さらに、その波の形を2乗すると、電子の存在する確率分布を示すことになる。これを「ボルンの確率解釈」という。電子の山と山、谷と谷が重なったところで、電子の密度が高く明るい。
電子は基本的には粒子であるが、その粒子をいったん波として計算するための考え方が確立解釈(統計的解釈)である。
ボルン によって提案された確率解釈の矛盾が無くて、今では最も正統的な解釈とされている。この考え方に基づいて、量子力学の全ての理論が組み立てられています。
波動方程式
1924年、ド・ブロイは光だけでなく電子や他の物質も波動性を持つということを唱えました。その波動を「物質波」と言いますが、電子の正体は波動で、見かけ上は粒子を示すという理論の構築に取り組みますが、うまくいきませんでした。1926年、シュレディンガーはド・ブロイの発想をもとにして物質波の波動方程式を構築しました。それが「シュレディンガー方程式」です。
この方程式を解くと、物質がどんな波形を持ち、その波が時間経過とともにどのように伝わるのかがわかります。
ボルンにより、波動関数ψの絶対値の2乗が、ある場所で粒子を見つける確率に比例するという波動関数の確率解釈が提案された。
波動関数は電磁波からの類推で導かれた概念であった。電磁波の振幅は電場や磁場の強さを表しているが、これらを2乗した量はエネルギーを意味している。電磁波に限らず、多くの場合、波の振幅の2乗は波のエネルギーを表すと考えられる状況になっている。なぜなら、正弦波が生じるためには変位に比例した復元力が働いているはずであり、その復元力を振幅の変位分だけ積分すればエネルギーを表すことになるが、この計算が振幅の2乗に比例するという結果となるからである。相対論によればエネルギーはすなわち質量であり、振幅の2乗が物体の存在する量を表すと考えるのはごく自然な発想なわけである。
しかし、物質が波のようにあらゆる場所に広がって存在していると考えるのには不都合がある。電子を標的にぶつける実験では、ぶつかった一点のみが光る。ぶつかるまでは多分どこかにあるはずだが、どこで見つかるかは分からない。そして、必ずある一点で見つかるのであり、波のようにぼんやりと全体的に反応するわけではない。
そこで、この「波動関数の絶対値の2乗」は「粒子をそこに見出す確率を表すのだ」ということで落ち着いた。
波動方程式は量子力学においてどのような意味と役割を持っているのでしょうか。
量子力学とは、我々の目には見えないミクロの世界を扱ったものです。この量子力学において重視されるのが、波動方程式になります。波動方程式の解として得られるのが、波動関数と呼ばれるものです。解として得られた波動関数は、固有の状態であるとするのが、波動方程式の意味だとされます。
波動関数における固有状態とは、電子の本質になります。逆に言えば、固有状態になれない関数は、電子の波動関数ではないのです。つまり、固有状態である波動関数を探すことが、すなわち量子力学の本質であると言えます。基本的にどんな関数であったとしても、作用素の影響を受けるとなにかしらの変化をします。反対に、作用した結果と作用そのものが一致するのは、一般的に考えれば特殊な状態なのです。しかし、電子における波動関数は必ず固有状態になります。量子の世界では一般的な変化が特殊で、特殊な固有状態が普通となってしまうのです。これが波動方程式の本質的な意味になります。
「波動関数は、固有状態になっている」 というのが、この方程式の意味です。方程式ですから、未知数を含みます。どれが未知かといえば波動関数です。どうやって解くのかというと、順番に適当な形の関数を作用素に作用させてみて、その結果が元の関数と同じ形になるかをチェックすればよいのです。 もちろん、ほとんどの場合、同じ形にはなりません。しかし、たくさん試行を続ければ、このチェックを通過する関数に遭遇します。そのとき方程式は解けたことになります。その関数が求める「波動関数」です。
ところで、シュレディンガーはいかにして壮大な理論へと止揚したのでしょうか。
ド・ブロイによる物質波の議論では、粒子として取り扱われる電子と物質波の関係が必ずしも明確でない。物質波は電子に付随すると言ったかと思うと、物質波の一部が凝縮して粒子状になるというイメージを語ることもあり、理論としての一貫性に欠ける。シュレディンガーは、粒子と波動の二面性に伴う曖昧さを避けるため、粒子概念を用いず、波動の一元論で話を進める道を選んだ。波動一元論の発想は、1927年にハイゼンベルクに手厳しく批判されることになるが、この時点では、方程式によって物質波を取り扱う唯一の手法であり、正しい選択だったと言える。粒子のイメージをきっぱり切り捨てたことによって、概念的な混乱に陥ることなく数学的な議論を全うすることができた。
残された研究ノートによると、シュレディンガーは、波動方程式を検討し始めた当初、相対論的な式を求めようとしたらしい。波動現象を扱う方程式としては、19世紀以降さまざまなタイプのものが考案されていたが、ローレンツ変換に対して不変性を保つ相対論的な方程式は、次の形のものが知られている。 (△ – ∂2/c2∂t2)ψ = f(ψ) (Δ:ラプラシアン) シュレディンガーはこのタイプの方程式(fがψの1次式のもの)をいろいろといじり回したようだが、間もなく、この式を使っていたのでは、水素原子のように電子が定常状態になるシステムをうまく扱えないと判断する。そこで、シュレディンガーはすぐに発想を切り替え、相対論にこだわらずに波動方程式を立てる決断をした。原子物理という当時の最先端分野において、「基礎方程式は相対論に従うべし」という原理的な要請を無視することは、ある意味で英断である。この決定の正当性は、その後に行われたエネルギー準位などの非相対論的な計算が充分に良い近似になることで確かめられた。
ここで、シュレディンガー本人が相対論にこだわらなかったにもかかわらず、シュレディンガー方程式そのものは相対論的な式だという点である。
シュレディンガーの洞察力が最高度に発揮されたのは、波動方程式は定在波(定常波)に関するもので充分だと見抜いたときである。
ド・ブロイは、水素原子核の周囲を円運動する電子に関して、「1周したときに同じ位相になる」という条件が満たされているときに定常状態が実現されると考えた。軌道半径をrとすると、軌道に沿った長さは2πrなので、ド・ブロイが与えた条件は、波長λの波が2πr進んだときに周回遅れの波と同じ位相になるという式、すなわち、 2πr = nλ(n:整数)・・・(1) となる。ド・ブロイは、すでに物質波の形式に関する議論を通じて、物質波の波長λと運動量mvの間に、関係式: mv = h/λ(h:プランク定数)・・・(2) があることを導いていた。式(1)と式(2)を組み合わせると、 mvr = nh/2π となるが、これは、1913年にボーアが水素原子模型を提唱した際に利用した量子条件と等しい。ボーアは、この量子条件を課すことによって、水素原子の線スペクトルに関するリュードベリの法則を導くことができたが、この量子条件が何を意味しているかは、理解の埒外に置かれていた。ド・ブロイは、物質波の干渉という直観的にわかりやすい議論によって、意味不明だったボーアの量子条件を理解する方向性を示したのである。 ド・ブロイが与えた式(1)は、冗長な博士論文の終わり近くに出てくるので、本気でこの論文を読破しようとした少数の物理学者にしか気づかれなかったが、シュレディンガーは見逃さなかった。しかも、粒子概念を捨てて波動だけの方程式を立てるべきだと考えていたシュレディンガーは、円運動する電子に付随して軌道上を進む波というド・ブロイのイメージが不適切であることにも気がついた。電子が存在しないとするならば、軌道上だけではなく原子核の周囲全体に拡がる波を想定しなければならない。そうなると、これは円軌道に沿って進む進行波ではなく、同じ場所で上下動を繰り返す定在波と見なすべきである。たとえ定在波であっても、軌道に相当する円周上で位相が少しずつずれながら振動していれば、そこで見ている限り進行波のように振舞う。しかし、全体としてみると、どこにも進んでいかずに原子核の周りに留まる定在波となっている。そして、定在波ならば、各地点での振幅を求める方程式には時間微分が含まれない。つまり、「時間に依存しない波動方程式」を考えれば良いのである。
シュレディンガーは、求めるべき波動方程式は波動関数に関して線形だと仮定した。その後に開発された量子力学的な解釈によれば、波動関数は重ね合わせの原理を満たす確率振幅となる。したがって、波動方程式が線形であることは、理論の原理的な要請となる。しかし、シュレディンガーが波動方程式についての考えを巡らしていた時点では、線形である必然性はなかった。むしろ、複雑な波動現象を可能にするには、非線形の方程式を考える方が自然である。にもかかわらず、シュレディンガーは線形の方程式しか扱わなかった。単に、線形方程式の方が簡単で解析しやすかっただけなのかもしれないが、そうであれば、議論のどこかに非線形に拡張することが可能だという留保をつけておくのが普通である。そうしなかったのは、論文に曖昧さを残したくないという彼の美意識からなのか? その辺りは定かでないが、これで波動方程式を求める目処が立った訳である。
ところで、初めて波動方程式を見たとき、どうして左右両辺に ψ(波動関数)が登場するのか、違和感を覚えるかもしれません。ψ(波動関数)がH(作用素)に作用した結果が、ψ(波動関数)の形と同じで変化しない、そういう関数を見つけられれば、 それが ψ(波動関数)です。 その ψ が示す「状態」において、E(固有値)という観測値が得られます。線形代数と量子力学は数理構造が同じなのです。
古典論では、微分方程式の解で複素数が出てきた場合は、ことごとく虚数部を捨て、実数部のみを現実の解とすることが常套手段です。しかし、波動力学では、複素数そのものが実在であると考えるのです。そして、この複素数の関係をシュレディンガーは「波動関数」と名付けました。波動関数はド・ブロイ波から生まれた概念です。
この方程式が正しいことを実証する方法は、様々な場合について、この微分方程式を解き、その結果が実験に一致することを確認しなければなりません。長い年月の検証に耐え、シュレディンガー方程式は、ニュートン力学において運動方程式が果たした役割を波動力学において担い続けているのです。
シュレディンガー方程式の波動関数は時間依存を持ちます。これが、加法的、線形、連続、可逆、確率の保存のようなシュレディンガー方程式の前提となる条件を満たすためには、虚部の導入以外の方法がありません。より一般化された数を用いることで、実際に見られる現象を説明できるようになる良いモデルです。
シュレディンガーの方程式は微分方程式であるが、空間と時間を扱っている。ただ、空間を微分するときには二階微分で、時間を微分するときには一階微分というように、空間と時間を区別して扱っている。
ディラックは、シュレディンガーの式に相対論を考慮に入れ整理すると、電子のエネルギーの解にはマイナスとプラスの2つがあることを発見した。反物質の存在を計算で証明したわけである。
シュレディンガー方程式では、時間微分の項に虚数が付いている。これが古典論的な波動方程式との一番の違いです。物質波 ψ というのが本質的に複素数を含む。
虚数とは、2乗すると-1になる数です。虚数と実数を組み合わせたものを複素数と言い、この方程式は複素数を含みますので、波動関数も、複素数の波であります。